A propos de la loi de Cauchy

Cette contradiction est valable, alors tout le chapitre des probabilités s'écroule.

C'est ici que vous faites erreur. Rien ne s'écroule.
Comme vous le savez peut-être, un théorème a des hypothèses et une conclusion. Prenons le théorème connu sous le nom de "loi des grands nombres". Dans ses hypothèses il y a que l'espérance de la valeur absolue de la variable aléatoire est finie. Eh bien, la loi de Cauchy ne vérifie pas cette hypothèse. Le fait qu'on a pas convergence dans le cas de la loi de Cauchy n'invalide absolument pas la loi des grands nombres.
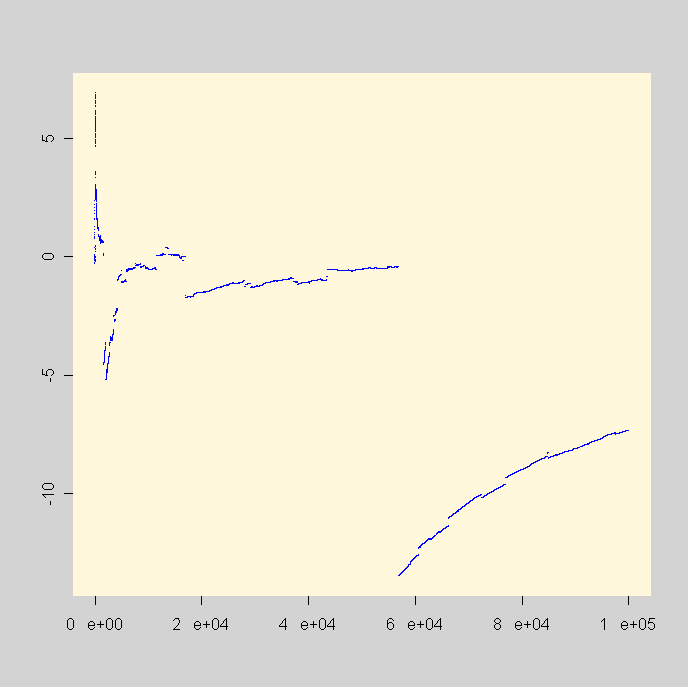
Vous me direz peut-être qu'un ingénieur se fiche de la loi de Cauchy parce qu'un ingénieur ne considère jamais que des grandeurs bornées. C'est vrai, mais même un ingénieur ne peut pas nier qu'il y a avec la loi de Cauchy, même tronquée, des phénomènes pathologiques qui peuvent se mettre en évidence  comme ici pour la moyenne empirique d'une série de valeurs suivant la loi de Cauchy :


Vous voyez clairement que la convergence est très perturbée par des phénomènes de saut.

Je crois que vous êtes un grand fan de Paul Lévy. Dans son article "Théorie des erreurs. La loi de Gauss et les lois exceptionnelles" de 1924, Paul Lévy consacre toute la deuxième partie à la loi de Cauchy (la vraie, pas tronquée, celle de densité (1/π) * 1/(1+x²)) et d'autre lois du même type pour lesquelles, je cite "l'erreur quadratique moyenne est nécessairement infinie". Rassurez-vous, ce n'est pas pour cela qu'il fait s'écrouler les probabilités !

Votre énoncé ""toute expérience de même protocole (ie loi uniforme) respecte la théorie des probabilités" est beaucoup trop imprécis.
Pour commencer, il y a toujours la même confusion entre "loi uniforme" et le fait qu'on ait une suite de variables aléatoires indépendantes de même distribution.  Ce n'est pas ça que veut dire "loi uniforme".
La loi de Cauchy fait bien partie de la théorie des probabilités, mais elle ne vérifie pas la conclusion de la loi des grands nombres. Si vous voulez contredire Paul Lévy sur ce point, je pense que vous ne faites pas le poids!

Pour ce qui est de l'espérance, je vous renvoie à votre cours de Levallois.
Levallois emploie la vieille terminologie (variable éventuelle au lieu de variable aléatoire, valeur probable au lieu d'espérance). Aussi il se limite au cas d'une variable aléatoire discrète. Dans le cas général la somme qui apparait est remplacée par une intégrale. Ainsi pour une variable aléatoire à densité f(x), l'espérance (ou valeur probable, pour suivre la terminologie désuète de Levallois) est l'intégrale de f(x) * x (ce qui remplace la somme des a_i * x_i

Ah au fait, que veut dire "problème de la caissière de cinéma" ?
Et que veut dire pour vous que la théorie des probabilités est respectée dans ce cas ?

Désolé, mais pourriez-vous m'expliquer plus précisément de quoi il s'agit ? Quel est le scénario ?

PS. En faisant une recherche sur "Prrobabilités problème de la caissière de cinéma" je suis tombé sur
https://www.maths-forum.com/lycee/probabilites-t128553.html
C'est bien de cela dont il s'agit ?

D'accord, c'est donc bien le problème dont il est question sur maths-forum. Comme il est écrit dans ce fil sur math-forum, ce problème est en fait l'habillage d'une marche aléatoire symétrique sur Z, l'ensemble des entiers relatifs. C'est un sujet très bien connu, sur lequel on peut trouver plein de références.
Je vais encore vous paraître désagréable, mais il m'est difficile de laisser passer sans réagir certaines affirmations.
D'abord, tout ceci n'a rien à voir avec la fin des molécules radioactives et la loi exponentielle que vous évoquiez plus haut. Où voyez-vous un quelconque rapport ?
Ensuite, d'après ce que je comprends, le "nombre de clients ayant pu avoir une place" correspond au temps d'attente pour qu'il ne soit plus possible de rendre la monnaie (2€50 dans le vieux fil de maths-forum, 5 € pour ce que vous décrivez  - le prix des billets de cinéma a bien augmenté !). Du point de vue des marches aléatoires, ça correspond au temps d'arrivée au niveau -1 en partant d'un niveau positif donné. Vous dites que ceci a une distribution gaussienne ?  En dehors même des problèmes discret/continu, je suis sûr que ceci est faux. Une des raisons : il est connu que, bien qu'il soit presque sûr qu'on va arriver à ce niveau -1, l'espérance du temps d'attente pour cette arrivée est infini. C'est absolument contraire au comportement d'une loi de type gaussienne ou binomiale ! Une référence pour ce que je viens d'écrire : https://fr.wikipedia.org/wiki/Marche_al%C3%A9atoire#Temps_de_premier_retour_%C3%A0_l'origine

Bonjour Dlzlogic,
J'ai fait une recherche avec "auteur : GBZM" sur ce forum, et j'ai pu retrouver ce fil :
https://dlz9.forumactif.com/t969-l-histoire-de-la-caissiere
C'est bien le même scénario que le fil sur maths-forum.
GBZM est un peu rude, mais je trouve que sur le fond il a parfaitement raison. Je vais essayer de prendre les choses par un autre bout.

Vous pensez qu'il s'agit ici d'une loi exponentielle parce qu'on attend quelque chose, à savoir que la caisse soit à court de billets de 5€ pour rendre la monnaie. C'est un point de vue simpliste qui ne résiste pas à une analyse sérieuse et scientifique de la situation.
Du point de vue marche aléatoire, ça revient à attendre un premier retour à 0. Il y a pour ça des résultats connus de tous les probabilistes et de la plupart des matheux, ceux qui ont un peu étudié les marches aléatoires. Je vous renvoie à un texte en français :
https://math.uni.lu/eml/assets/reports/contignon-leite.pdf
Dans le paragraphe 2.3.3 "Retours à l'origine", au théorème 5 page 19, il y est établi que la probabilité qu'il n'y ait pas de retour à l'origine (il y a une coquille malencontreuse dans l'énoncé, mais la formule est claire) jusqu'à l'instant 2n compris est u_n= (1/2ⁿ) * C_2nⁿ (où C_2nⁿ est le nombre de combinaisons de n parmi 2n). C'est la probabilité de "survie" de la caisse jusqu'à l'instant 2n. Un petit calcul facile montre alors que le nombre de survivants à l'nstant 2(n+1) est égal au nombre de survivants à l'instant 2n divisé par  1  + 1/(2n) + o(1/n) où o(1/n) est négligeable devant 1/n quand n tend vers l'infini. Ce nombre varie avec n et tend vers 1 quand n tend vers l'infini.
Or vous devriez savoir qu'une caractéristique de la loi exponentielle ou de la loi géométrique est que le nombre de survivants est divisé sur un laps de temps Δt donné entre t et t+Δt par une constante > 1, ne dépendant pas de t.
On n'a donc ni loi exponentielle ni loi géométrique dans le cas de la caisse. Les lois exponentielles et géométriques sont des lois sans mémoire : la probabilité de survie ne dépend pas de l'histoire passée. Un peu de réflexion sur le cas de la caissière montre que ce n'est pas valable ici : si la caisse a déjà survécu pendant longtemps, alors il est fort probable qu'elle a amassé un bon paquet de billets de 5€ et donc que ses perspectives de survie s'en sont améliorées. Ceci est quantifié précisément par le petit calcul que j'ai fait plus haut.
Certes, le nombre de caisses survivantes décroit vers 0 (comme le nombre d'atomes radioactifs). Mais ce n'est pas pour cela que la décroissance est exponentielle !

Non, cette loi de Cauchy ne converge pas correctement. Sur quel argument vous basez vous pour dire cela ?
Si vous tronquez la loi de Cauchy pour avoir une variable aléatoire bornée, alors oui ça va converger (péniblement sauf si vous faites une troncature sévère). Mais pour la vraie loi de Cauchy, pas de convergence.
J'ai cité au début de ce fil l'article de Paul Lévy que vous pouvez trouver ici :
http://www.numdam.org/article/BSMF_1924__52__49_1.pdf
Au début de la seconde partie de l'article (bas de la page numérotée 68), Paul Lévy écrit que " Le but de cette seconde partie est d'étudier les lois exceptionnelles, c'est-à-dire n'appartenant pas au domaine d'attraction de la loi de Gauss ". Ceci veut dire que ces lois ne satisfont pas à la conclusion de ce que vous appelez deuxième théorème de Bernoulli, autrement dit que la moyenne d'un grand nombre de variables indépendantes distribuées suivant cette loi ne converge pas vers la loi de Gauss. Et Lévy montre que la loi de Cauchy n'est justement pas dans le domaine d'attraction de la loi de Gauss : la moyenne d'un grand nombre de variables suivant la loi de Cauchy suit encore la loi de Cauchy, et ne converge absolument pas vers la loi de Gauss.
Maintenant, si vous voulez prétendre que Paul Lévy a tort ...

Vous vous obstinez à contredire Paul Lévy ; c'est vraiment incompréhensible. Vous pouvez le lire : j'ai donné le lien sur son article.
Non, la loi de Cauchy ne converge pas vers la moyenne. Oui, la loi de Cauchy tronquée (variable aléatoire bornée) converge ; mais ce n'est pas la loi de Cauchy.
Les techniques de discussion des matheux, c'est de donner des arguments précis et vérifiables. Effectivement, c'est différent de votre technique de discussion.

Dlzlogic a écrit:Je connais bien les techniques de discussion des matheux.

Oui, les matheux donnent des arguments, des preuves vérifiables, des références précises.
Toutes choses qui te sont parfaitement inconnues.

Alors donnez un exemple d'utilisation de la loi de Cauchy

Ce n'est pas la question.

La question c'est : est-ce que la moyenne d'un grand nombre de loi de Cauchy indépendantes convergent vers un nombre (l'espérance: LGN),
et l'écart à ce nombre, multiplié par sqrt(n) converge-t-il en loi vers une loi normale. La réponse est non, comme prouvé par Lévy lui-même
dans le document cité ci-dessus.

Mais puisque Dlz SAIT que ce n'est pas vrai, il peut affirmer "La loi de Cauchy est une loi exceptionnelle, c'est à dire que c'est une exception à la règle générale. Elle converge un peu moins vite que la loi normale mais elle converge vers la moyenne. " et cela devient la VERITE, puisque l'on sait bien que c'est "comme Dlz veut", et Lévy n'a qu'à se rhabiller.


P.S: la loi de Cauchy n'est certainement pas un "contre-exemple" de la loi des grands nombre, puisque elle ne vérifie pas les hypothèses du théorème.
Le fait qu'elle ne vérifie pas les conclusions du théorème ne remet donc pas en question sa véracité, ni son utilité. Ouf, les probabilistes sont sauf.

Mais bon, cette subtilité paraît hors d'atteinte, essaye donc déjà de retenir ce qu'est une "loi uniforme" (tu t'es encore trompé), et une espérance (idem).

Décidément, Dlzlogic, cette fichue loi de Cauchy vous perturbe beaucoup. Si ça vous amène à lire Lévy, c'est déjà une preuve de son utilité. Mais qu'en retiendrez-vous ?
La loi de Cauchy fournit à Paul Lévy un très bel exemple de loi stable qui n'appartient pas au domaine d'attraction de la loi de Gauss. Ce coquin de Lévy a aussi laissé son nom à une autre loi stable qui n'est pas non plus dans le domaine d'attraction de la loi de Gauss : la loi de Lévy. Décidément, on dirait que Paul Lévy s'ingénie à vous embêter !

À propos de la loi de Cauchy, vous pouvez lire cette page : https://stats.stackexchange.com/questions/416304/why-is-the-cauchy-distribution-so-useful. On y lit qu'elle est utilisée en physique et même en finance.

Bonjour Dlzlogic,
Toujours aussi désagréable, à ce que je vois. Devrais-je aussi faire une analyse psychologique des raisons de votre aversion pour les mathématiques et les mathématiciens ?

Bien, revenons au sujet. Vous m'avez posé la question de l'utilité de la loi de Cauchy. Je vous ai répondu sur son importance théorique, en particulier pour Paul Lévy. Je vous ai aussi donné en lien une page de réponse justement à la question "Pourquoi la loi de Cauchy est-elle si utile ?". Peut-être avez-vous eu du mal à lire les réponses parce que la page est en anglais. Permettez-moi de vous en proposez une traduction :

La distribution de Cauchy est importante en physique (où elle est connue sous le nom de distribution de Lorentz) car c'est la solution de l'équation différentielle décrivant la résonance forcée. En spectroscopie, c'est la description de la forme des raies spectrales soumises à un élargissement homogène dans lequel tous les atomes interagissent de la même manière avec la gamme de fréquences contenue dans la forme de la raie.

Applications:
    Utilisé en théorie mécanique et électrique, en anthropologie physique et en problèmes de mesure et d'étalonnage.
    En physique, on parle de distribution lorentzienne, où il s'agit de la distribution de l'énergie d'un état instable en mécanique quantique.
    Également utilisé pour modéliser les points d'impact d'une ligne droite fixe de particules émises par une source ponctuelle.

En plus de son utilité en physique, la distribution de Cauchy est couramment utilisée dans les modèles financiers pour représenter les écarts de rendement par rapport au modèle prédictif. La raison en est que les praticiens de la finance hésitent à utiliser des modèles qui ont des distributions à queues légères (par exemple, la distribution normale) sur leurs rendements, et ils préfèrent généralement aller dans l'autre sens et utiliser une distribution avec des queues très lourdes (par exemple, la distribution de Cauchy). L’histoire de la finance est parsemée de prédictions catastrophiques fondées sur des modèles dont les distributions n’avaient pas de queues suffisamment lourdes. La distribution de Cauchy a des queues suffisamment lourdes pour que ses moments n'existent pas, et c'est donc un candidat idéal pour donner un terme d'erreur avec des queues extrêmement lourdes.

Je vous rappelle que le fil que vous avez initié s'appelle "à propos de la loi de Cauchy". Vous avez déjà introduit une diversion en parlant de "la simulation du problème de la caissière de cinéma".  Si maintenant vous voulez parler du fameux "paradoxe de Bertrand" ou de l'aiguille de Buffon, je veux bien, mais alors faites-le dans un autre fil. Sinon, on ne va plus s'y retrouver. Ici, concentrons-nous sur la loi de Cauchy s'il vous plait.

PS. Une autre page où l'on parle de la loi de Cauchy dans le contexte de la spectroscopie :
https://en.wikipedia.org/wiki/Spectral_line_shape
Désolé, cette page est encore en anglais. Vous n'y trouvez pas le nom de Cauchy, mais il y est fait mention de façon répétée de la distribution lorentzienne qui est le nom que les physiciens ont l'habitude de donner à la distribution de Cauchy.